Video: https://www.youtube.com/watch?v=c0AkCcUzcj8
Print it yourself: https://chandler.io/posts/2025/03/print-it-yourself-illegal-slice-cube/
The Illegal Slice Cube continues my exploration of finite group theory in twisty puzzles. It combines two unusual concepts:
Oskar van Deventer’s Illegal Cube
- Fudging permits 90° turns, which normally wouldn’t be allowed on a 3x3 pentagonal prism.
Slice-only puzzles (like Slice Rex Cube)
- Opposite sides turn simultaneously - like a 3x3 Rubik’s cube with middle turns only.
Unlike some of the previous puzzles in this series, this one is pretty difficult to solve.
The Crammed Cube is an internally geared twisty puzzle that expresses the Mathieu M11 group over its 12 edge pieces. The puzzle features a modified Compy Cube mechanism with 6 axes, which are mechanically linked into two sets using universal joints and gears. It is called the ‘Crammed Cube’ because, while the axis system would normally have 11 moving edges, I’ve crammed an extra one into the red/white edge and lifted the corner angle to make space. This edge duplication is necessary to make the group actions fit over cubic geometry.
The Fano Gem is a twisty puzzle that I designed to showcase the symmetries of the Fano Plane, which is a familiar object in combinatorics, coding theory, and algebra. The Fano Plane is the smallest possible finite projective plane, constructed from 7 points and 7 lines, where each line contains exactly 3 points.
From the red face (pictured left), the numbers on the corners of the puzzle match up with the numbers on the plane (with number 7 on the back of the puzzle, out of view).
The Quaternion Cube is a rather easy-to-solve puzzle that I designed to visually demonstrate the Quaternion Group Q₈.
The puzzle turns over the top 4 vertices of a cube, with 1:2 gearing connecting the opposing corners. There are linear slides under the edge pieces that prevent the static corners from blocking the overall movement.
The puzzle has 24 possible positions, which express the group SL(2,3). SL(2,3) contains the Quaternion Group (Q₈) as a subgroup, and these Q₈ states are expressed over the 8 edges whenever the corners are solved.
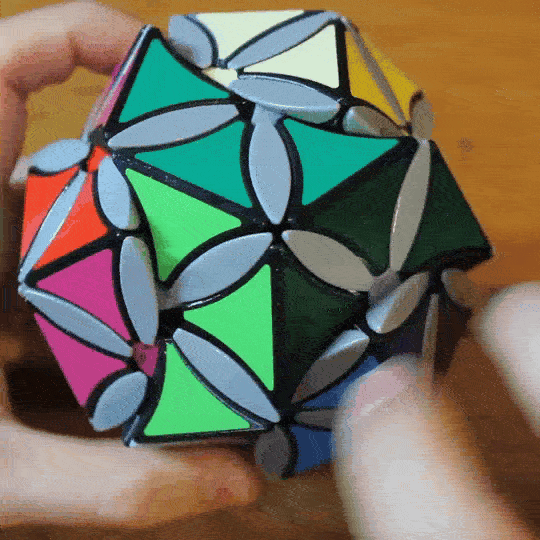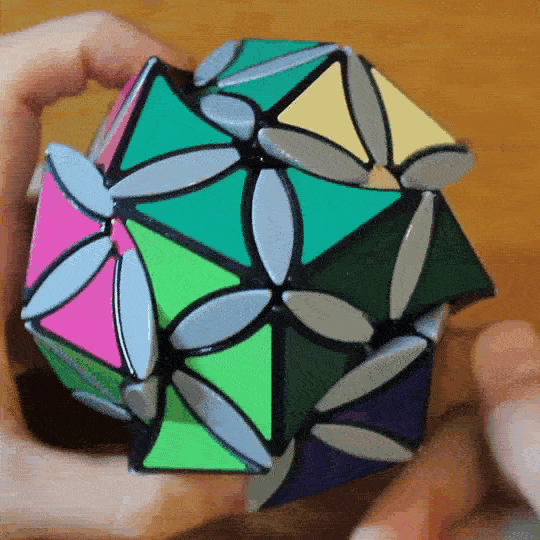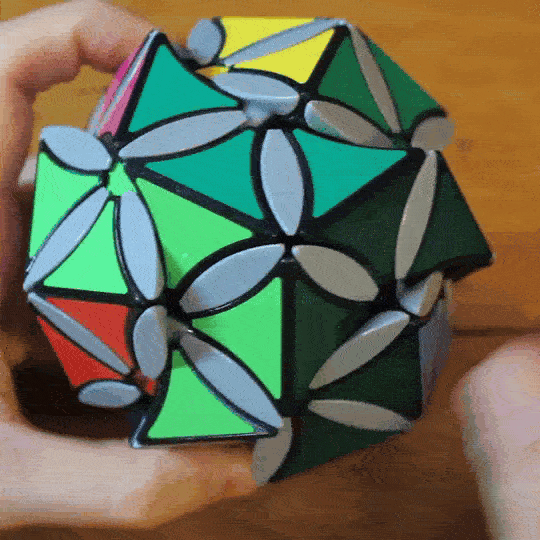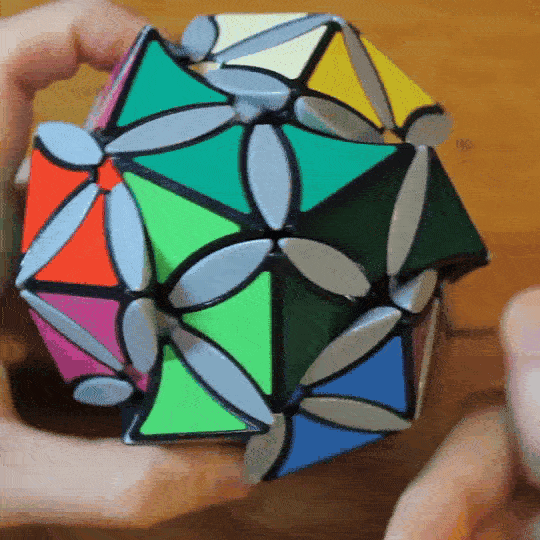
DoDot M12
The DoDot M12 is a twisty puzzle that mechanically demonstrates Mathieu group M12. It’s a modification of my original vertex-turning dodecahedron where sets of three turning axes are geared together internally. This gearing was chosen to greatly reduce the number of possible permutations of the ‘dot’ pieces, which behave according to the rules of the 12-element M12 permutation group. The edge pieces of the puzzle behave as 6 disjoint orbits of 5 pieces, which makes them easy to solve. I greyed out the petals to avoid making the puzzle too complicated.
The DoDot puzzle is a variation of the Bauhinia Dodecahedron inspired by David Pitcher’s OctaDot.
The Antler Cube is a modification of the Nón Lá cube that unlocks new moves and a more difficult solve.
Quirky Gem III Puzzle
Quirky Gem II Puzzle
Quirky Gem I Puzzle
