This video outlines the entire process of designing the Rocking Cube (PSL₂(13)), including group selection, data refinement & visualization, and mechanical implementation.
The Rocking Cube is an internally geared twisty puzzle that expresses the group PSL₂(13) over its 14 edge pieces. This was a difficult puzzle to design, and I published a YouTube video outlining the process.
The Crammed Cube is an internally geared twisty puzzle that expresses the Mathieu M11 group over its 12 edge pieces. The puzzle features a modified Compy Cube mechanism with 6 axes, which are mechanically linked into two sets using universal joints and gears. It is called the ‘Crammed Cube’ because, while the axis system would normally have 11 moving edges, I’ve crammed an extra one into the red/white edge and lifted the corner angle to make space. This edge duplication is necessary to make the group actions fit over cubic geometry.
Originally published 2025-03-06
Updated 2025-11-05
Video
Solving Guide
Photos
The M12 Cube is an internally geared twisty puzzle that expresses the Mathieu M12 group over its 12 edge pieces.
Video
Solving Guide
Photos
Updated 2025-07-31
The Quaternion Cube is a rather easy-to-solve puzzle that I designed to visually demonstrate the Quaternion Group Q₈.
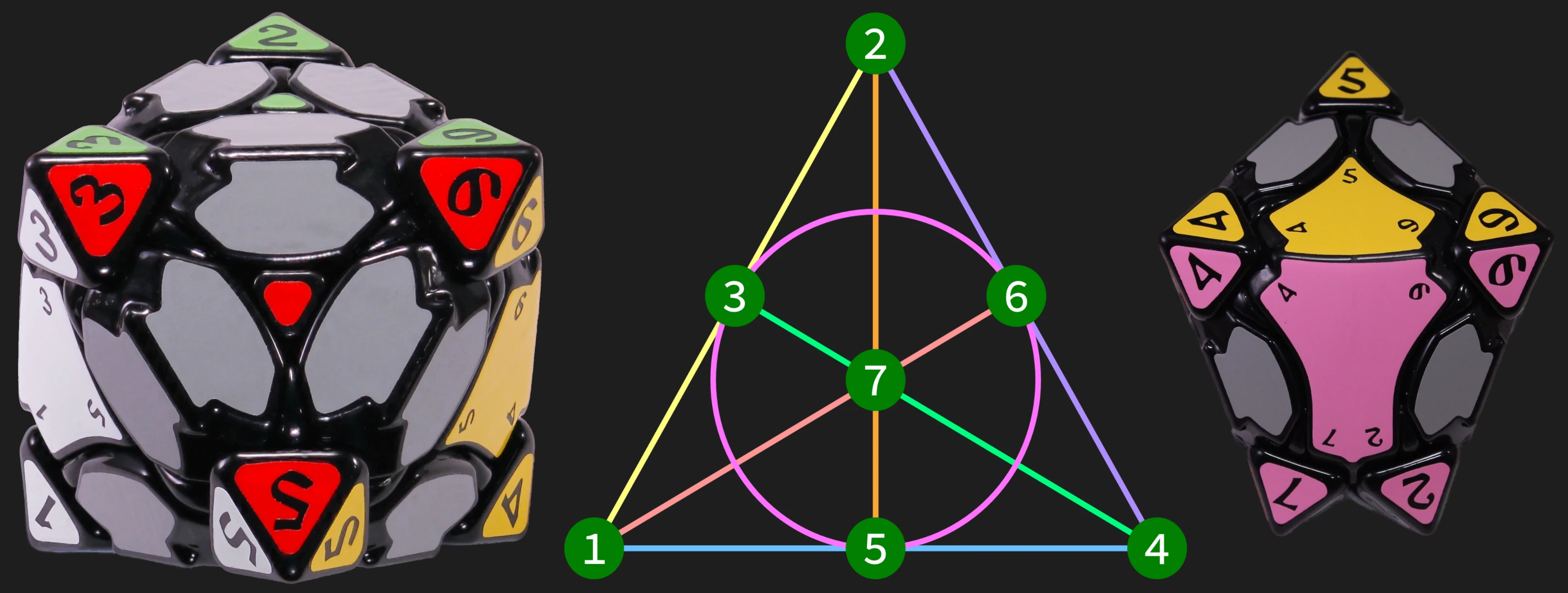
The Fano Gem is a twisty puzzle that I designed to showcase the symmetries of the Fano Plane, which is a familiar object in combinatorics, coding theory, and algebra. The Fano Plane is the smallest possible finite projective plane, constructed from 7 points and 7 lines, where each line contains exactly 3 points.
