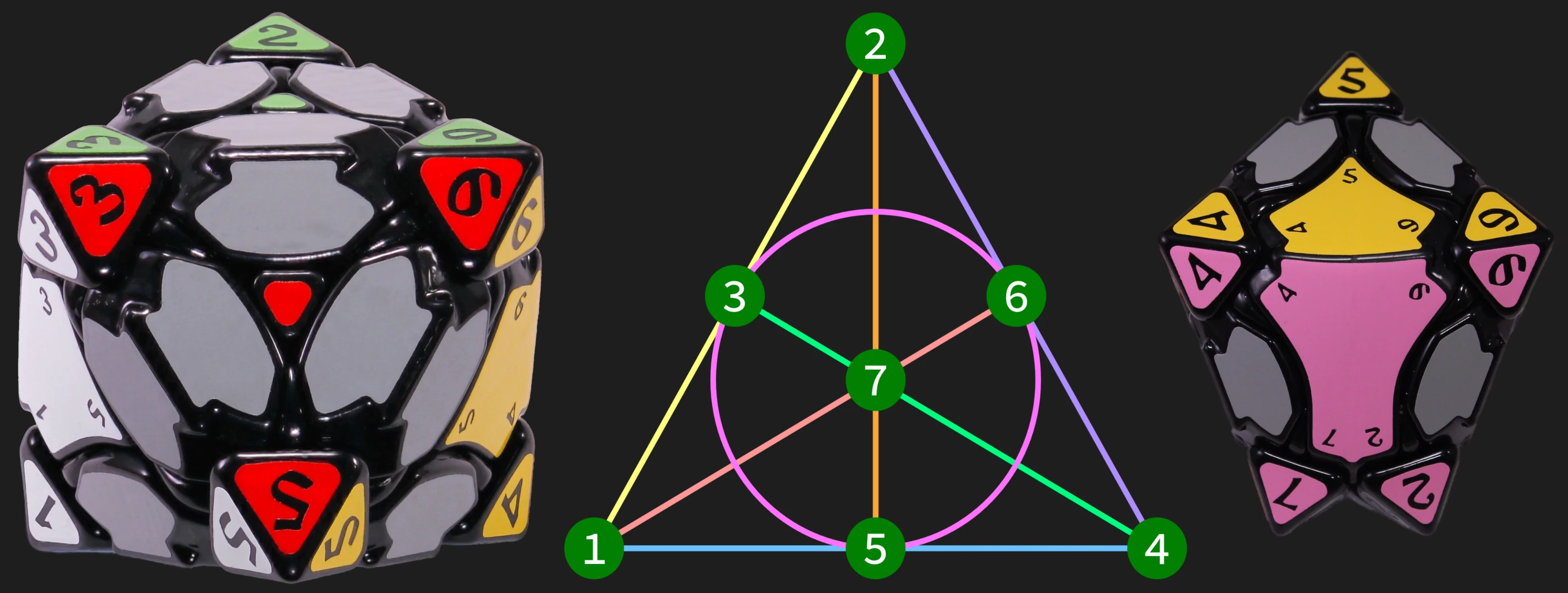
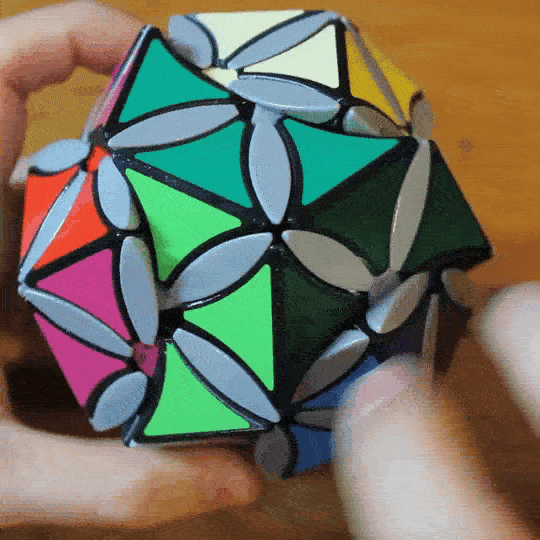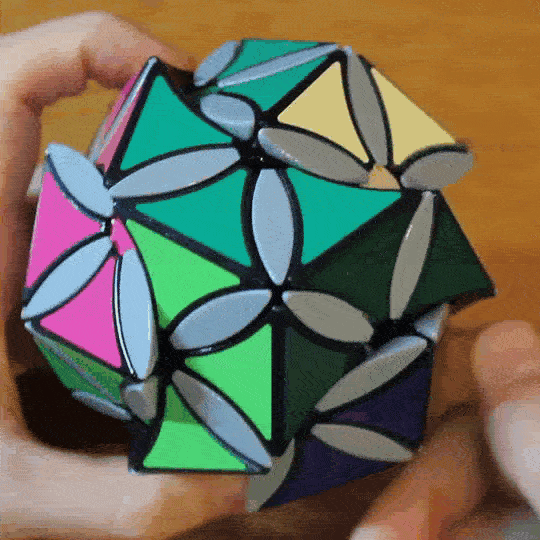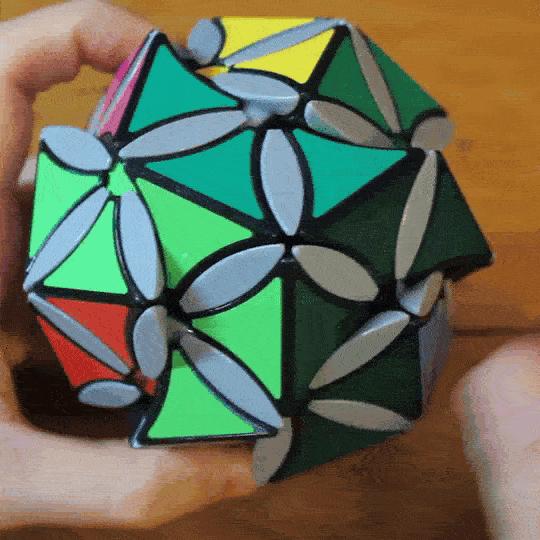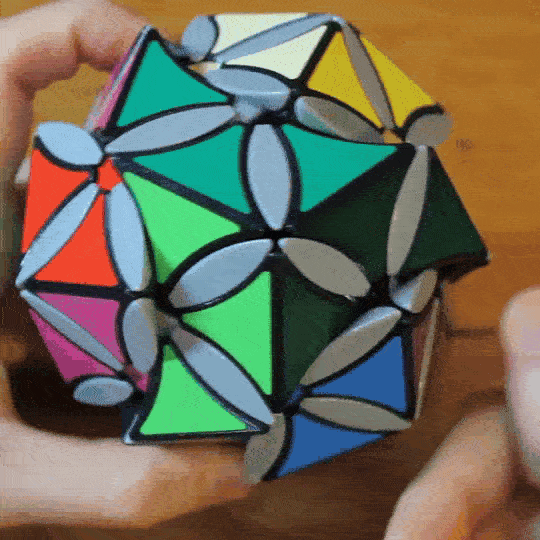M12 Cube & Simulator

The M12 Cube is an internally geared twisty puzzle that expresses the Mathieu M12 group over its 12 edge pieces.

Simulator

Animation Speed

Video

Construction

This axis system and its mirror are the only ways to express the M12 group on a Compy Cube, unlike dodecahedral faces, where the DoDot M12 is one of many possible configurations.

The puzzle has a set of 3 and another set of 4 axes that are geared together internally. They don’t all turn in the same direction, so a 4-layer gearbox was required to make it work.

Gearbox

Stats

Weight: 220 g
Edge length: 70 mm
Reachable positions: 3 × 3 × 95040 = 855,360
God’s number: 19

Solving Guide

General Hints

Since there are essentially only 2 available moves on this puzzle at any given time, it’s useful to develop a toolbox of short sequences with known actions that can be combined into a full solution. In developing my solution, I first created a table of sequences and their actions for all commutators ranging 1-6 moves.

Understanding the orders of each possible M12 state is essential for developing a solution. For example, sequences that produce a simultaneous 2-cycle and 8-cycle are easy to find, but not especially useful. However, they can be executed twice to produce the rarer dual 4-cycle. As another example, to develop a corner untwist algorithm, simply find any sequence that leaves a corner twisted but has a cycle order that’s not divisible by 3.

Working out a solution is a difficult but rewarding process. The simulator on this page automatically tracks cycles and moves, which can save a lot of time.

Full Solution

If you don’t want to start from scratch, my own step-by-step solution follows:

Introduction

Pieces and slots are referenced by their color combinations - for example, the Yellow & Green edge piece (or slot) is YG.

It’s helpful to hold the cube in this orientation when performing algorithms:

Hold cube by the static corner with thumb on green

Corners X and Y are on the left edge (the RWB and OBW corners respectively). The notation X in an algorithm means to turn corner X clockwise as pictured, and X' counter-clockwise. The same goes for corner Y.

The edge slots adjacent to your thumb (the static green sticker) are YG and GO, which will be solved in steps 1 and 2.

Looking at the RGW corner, the two red-side slots furthest from you are BR and YR. These will be solved in step 3.

1. Insert 1st piece intuitively

The first step is to insert the YG edge piece into its slot.

2. Insert 2nd piece using 11-cycle

The next piece to solve is GO, which can be done intuitively, or by repeating this sequence that fixes YG and cycles all of the other edges:

11 cycle - (GR -> YO -> WO -> BR -> WG -> WR -> WB -> YB -> YR -> BO -> GO)
  5 moves: X Y X' Y' X

Note: The cycle description in parentheses indicates that after execution, the piece in the GO slot will move to the GR slot, the piece in GR to the YO slot, and so on.

3. Insert 3rd and 4th pieces

Next, solve YR and BR in any order. This can be done one at a time using the listed quaternion algorithms (see Quaternion Algorithms), and a conjugate that temporarily puts either the YR or BR slot into their cycle paths while leaving the other fixed pieces alone.

If the RBY corner already has YR or BR surrounding it, just turn it into place.
Use conjugate Y or Y' to temporarily move an unwanted piece into the YB slot.
Identify a quaternion algorithm cycle that puts the desired piece (YR or BR) into the YB slot, and execute it. For example, if the desired piece is in the WB slot, use Qᵢ to move it to YB.
Ensure the YB slot now contains the selected piece, and undo the conjugate.
If necessary repeat for the other piece.

4. Solve quaternion state

Now that 4 edge pieces are solved, the remaining 8 are in a ‘quaternion state’. Use the appropriate quaternion algorithm to solve the remaining edges.

5. Untwist corners

The algorithms in this solution do not preserve the orientation of the corners, so the corners must be ‘untwisted’ after the edges are solved.

Twist X clockwise:
 24 moves: (X Y X Y X' Y)×4
Twist X counter-clockwise:
 24 moves: (Y' X Y' X' Y' X')×4

Twist X clockwise and Y counter-clockwise:
 16 moves: (X' Y)×8
Twist X counter-clockwise and Y clockwise:
 16 moves: (Y' X)×8

Quaternion Algorithms

On an M12 puzzle, solving any arbitrary set of 4 pieces leaves the remaining 8 pieces in one of 8 states, which I call ‘quaternion states’. The 8 pieces may then be solved optimally using algorithms corresponding to the quaternions i, j, k, and -1, and their inverses.

These particular quaternion algorithms fix YG, GO, YR, and BR, cycling the rest:

 Qᵢ  - (BO -> WR -> WO -> GR), (WG -> YO -> WB -> YB)
  12 moves: (Y  X' Y X' Y X )×2
  Inverse:  (X' Y' X Y' X Y')×2

 Qⱼ  - (WG -> WO -> WB -> BO), (GR -> YO -> WR -> YB)
  18 moves: (X Y' X') (Y  X' Y X' Y X )×2 (X Y X')
  Inverse:  (X Y' X') (X' Y' X Y' X Y')×2 (X Y X')

 Qₖ  - (WG -> WR -> WB -> GR), (WO -> YO -> BO -> YB)
  18 moves: (X Y X') (Y  X' Y X' Y X )×2 (X Y' X')
  Inverse:  (X Y X') (X' Y' X Y' X Y')×2 (X Y' X')

 Q₋₁ - (WG <-> WB), (BO <-> WO), (WR <-> GR), (YO <-> YB)
  24 moves: (Y X' Y X' Y X)×4

M12 State Breakdown

The M12 group has 95040 possible states. The following table shows the frequency of each type of cycle.


17280: single 11-cycle
15840: single 2-cycle, single 3-cycle, single 6-cycle
11880: single 2-cycle, single 8-cycle
11880: single 4-cycle, single 8-cycle
 9504: dual 5-cycles
 9504: single 2-cycle, single 10-cycle
 7920: dual 6-cycles
 2970: dual 2-cycles, dual 4-cycles
 2970: dual 4-cycles
 2640: quadruple 3-cycles
 1760: triple 3-cycles
  495: quadruple 2-cycles
  396: 6p 2-cycles
    1: solved