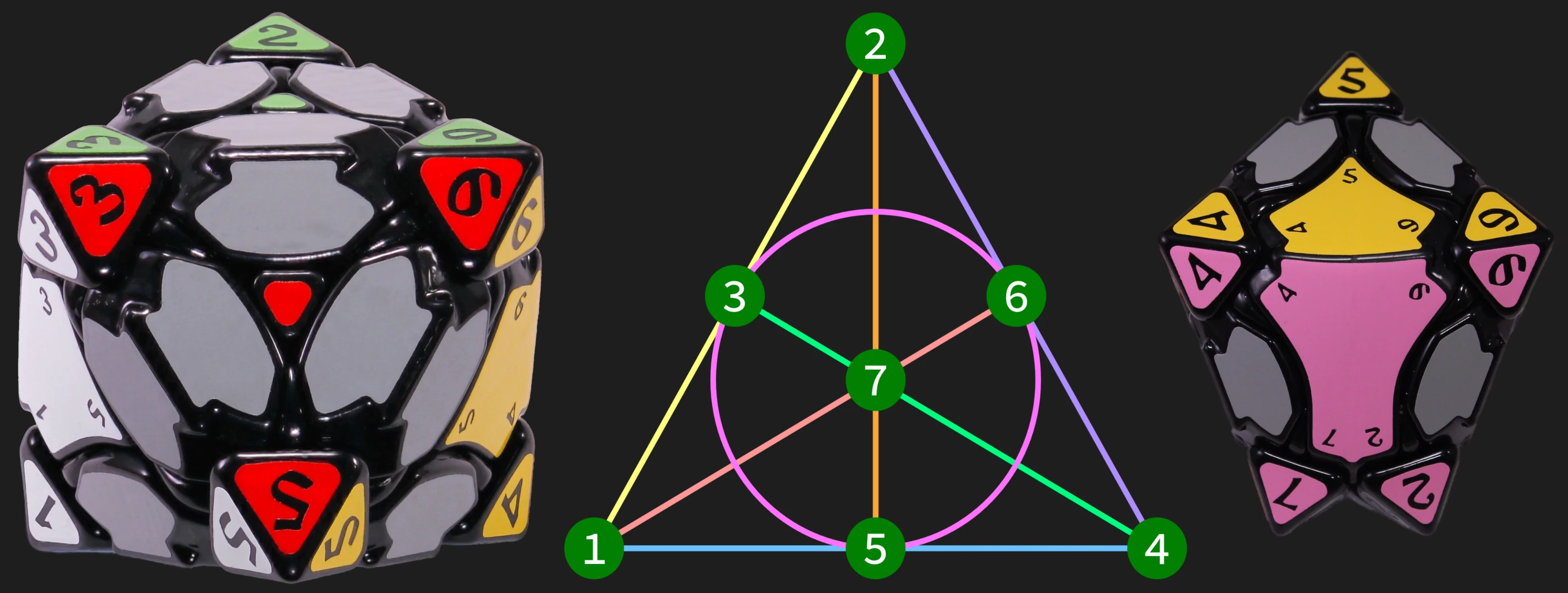
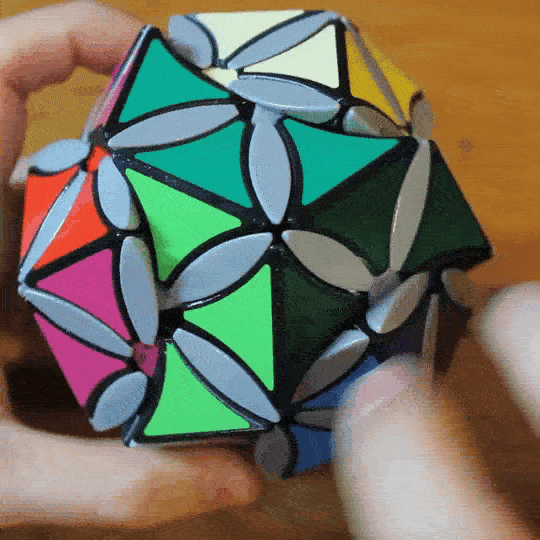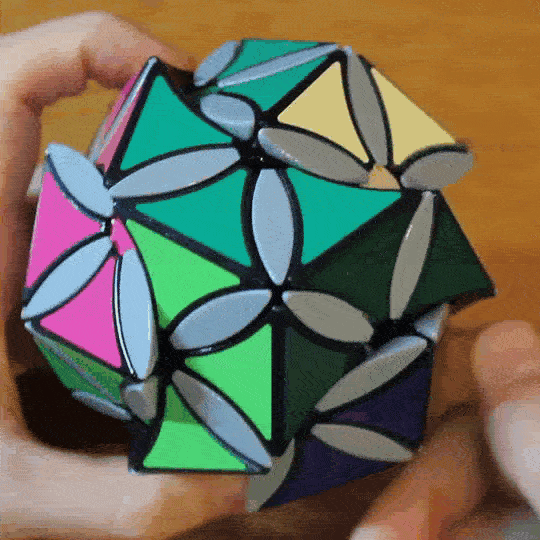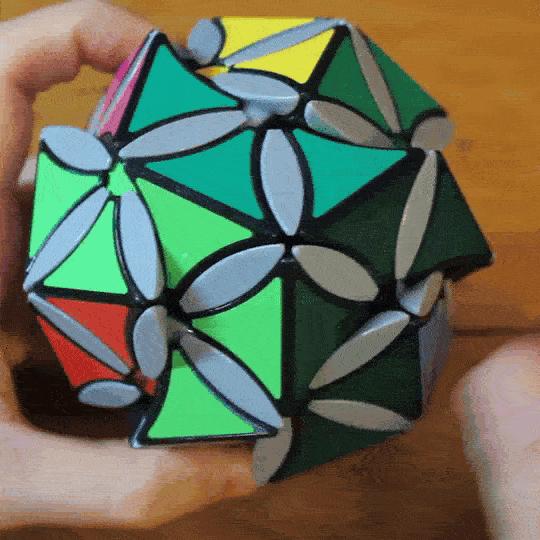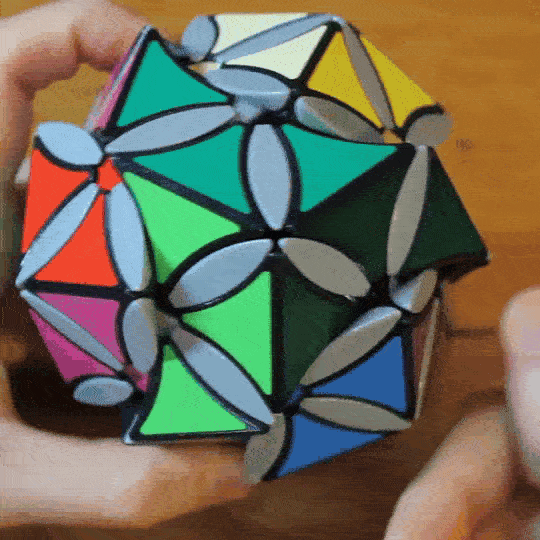The Crammed Cube is an internally geared twisty puzzle that expresses the Mathieu M11 group over its 12 edge pieces. The puzzle features a modified Compy Cube mechanism with 6 axes, which are mechanically linked into two sets using universal joints and gears. It is called the ‘Crammed Cube’ because, while the axis system would normally have 11 moving edges, I’ve crammed an extra one into the red/white edge and lifted the corner angle to make space. This edge duplication is necessary to make the group actions fit over cubic geometry.
Simulator
Construction
The puzzle’s six corner axes are divided into two groups of three that are mechanically linked. When a central corner is rotated clockwise, the diagonally opposite corners rotate counterclockwise simultaneously.
The mechanism combines gears and universal joints that pass through the puzzle’s core.
Video
Full video coming soon.
Turning demonstration:
Theory
The edge pieces express the M11 group over 12 points. In the natural 11-point representation of M11, stabilizing one point at a time produces a clear factorization:
- Degree 11 — sharply 4-transitive
- 7920 = 11×10×9×8 : M11 → M10 → M9 → M8 (Q8)
However, the 12-point representation used in this puzzle has a less intuitive point stabilizer series:
- Degree 12 — 3-transitive
- 7920 = 12×11×10×6 : M11 → PSL(2,11) → A5 → D₆
The groups in this chain have unusual properties. PSL(2,11) over 11 points is the symmetry group of the vertices of the 11-cell, while the Alternating group A5 over 10 points corresponds to the face symmetries of the projective icosahedron.
Puzzle Specifications:
- Total states: 71,280 (3×3×7920)
- God’s number: 20 (18 without corner stickers)
- Undistorted edge length: 70mm
- Weight: 240g
Solving Guide
General Hints
The Crammed Cube can be solved one piece at a time until it’s reduced to the dihedral group D₆, where 9, 6 or 0 pieces will appear unsolved.
The process for solving each piece is enhanced by understanding the M11 subgroup that’s being expressed at each step. The point stabilizer subgroups are each a symmetry group of some geometric object.
Full Solution
Below is an un-optimized step-by-step solution that should be easy to follow. It’s designed to keep the corners solved as often as possible, which makes the edges easier to track but results in long sequences.
Introduction
Pieces and slots are referenced by their color combinations. For example, the Yellow & Blue edge piece is YB. As pictured, YB is in the Blue & Red BR slot. There are two undifferentiable WR pieces - these will be solved first to get them out of the way.
It’s helpful to hold the cube in this orientation when performing algorithms:
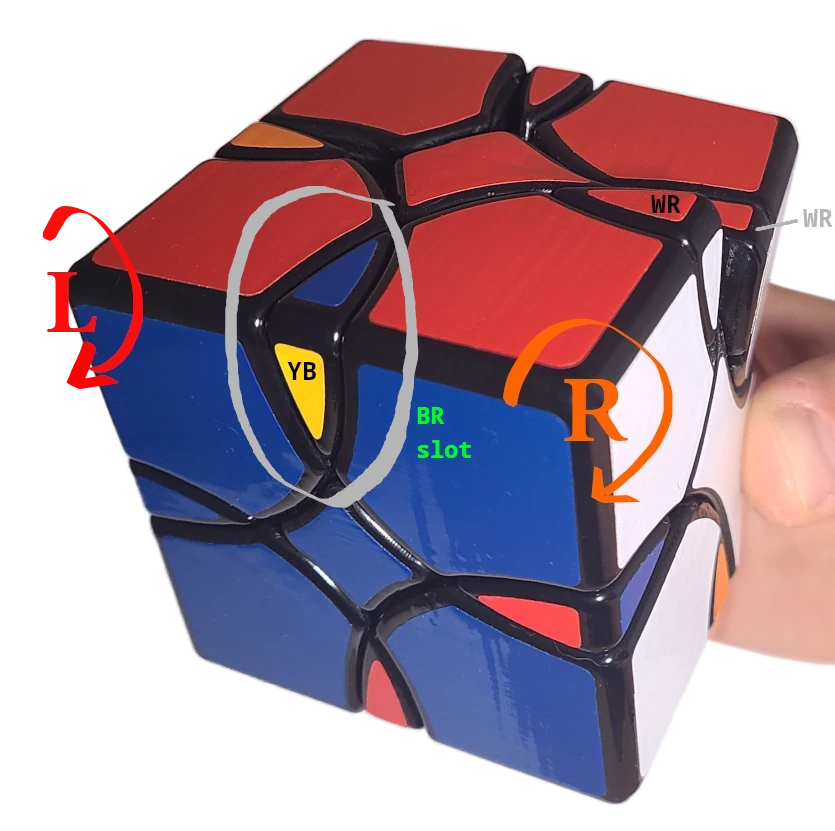
Corners L and R are on the edge opposite your hand (the YWB and WBR corners respectively).
The notation L in an algorithm means to turn corner L clockwise as pictured, and L' counter-clockwise. The same goes for corner R.
1. Insert 1st piece intuitively
The first step is to insert the top WR edge piece into its slot (the one labeled with grey text). Fixing one piece reduces the solution space to PSL(2,11) with order 660. Make sure corner R is solved.
2. Insert 2nd piece using 11-cycle
The second WR piece can be inserted intuitively, or using a 11-cycle that fixes the first piece and cycles the rest. Execute it repeatedly until you notice that both WR pieces are in their correct positions.
11-cycle: WO → GR → YG → YO → BR → BO → YB → WG → YR → WB → WR
4 moves: L R L' R
inverse: R' L R' L'
Note that this may leave the R corners unsolved. Another sequence may be used ‘untwist’ them without affecting the WR pieces:
Twist R clockwise
11 moves: L R' L' R L R L' R' L R L'
inverse: L R' L' R L R' L' R' L R L'
3. Check conjugacy class and flip indistinguishable pieces
Despite the two WR pieces being identical, the puzzle is not solvable unless they are in their correct positions. You must check whether or not they are correct by tracking the cycles in unsolved edges.
See Listing Cycles Procedure for the steps for listing out the cycles.
Correct cases:
- Quadruple 2-cycles, e.g. (
WB↔GR), (BR↔YG), (WO↔YO), (BO↔YB) - Triple 3-cycles, e.g. (
WO→BO→GR), (WG→BR→YG), (WB→YB→YO) - Dual 5-cycles, e.g. (
WO→BR→YB→YO→GR), (WG→BO→WB→YG→YR)
Incorrect cases (WR pair is flipped):
- Triple 2-cycles, e.g. (
WO↔GR), (BR↔YG), (WB↔YO) - 3-cycle and 6-cycle, e.g. (
BO→YB→YR), (BR→YO→WO→YG→WB→GR) - 2-cycle and dual 4-cycles, e.g. (
BR↔YR), (WG→YO→YG→GR), (BO→WO→WB→YB)
If your puzzle looks like something in the first list, no action is needed. If it matches the second list, the WR pieces need to be flipped; execute the following sequence to flip them:
Flip WR pieces
12 moves: (L R' L' R)×2 (L' R' L R)
4. Solve icosahedron or reduce further
With two pieces correctly placed, the remaining pieces mimic the symmetry group of the hemi-icosahedron. You could visualize this as a 3D icosahedron with each pair of opposide faces numbered 1-10. Looking back at the list above, we have 5-cycles, 3 cycles, or swaps, which are all possible to perform just by rotating the icosahedron on its vertices, faces, or edges respectively.
You can download a printable icosahedron template that assigns the remaining edge piece colors to its faces, if you’d like to visualize the remainder of the solution.
The quickest icosahedral rotation to perform is denoted A, a 5-cycle.
Move A: (YO → YB → BR → WO → GR), (YG → WB → BO → WG → YR)
5 moves: R L R L' R
inverse: R' L R' L' R'
Move A×2:
10 moves: R' (R' L R L')×2 R
inverse: R' (L R' L' R)×2 R
You can get some different 5-cycles by conjugating A:
Move B: (BO → WO → WB → YO → YG), (WG → YB → GR → BR → YR)
16 moves: L' R L' R' L R (R' L R L') R' L' R L R' L
inverse: L' R L' R' L R (L R' L' R) R' L' R L R' L
Move B×2:
20 moves: L' R L' R' L R (R' L R L')×2 R' L' R L R' L
inverse: L' R L' R' L R (L R' L' R)×2 R' L' R L R' L
Move C: (BO → YB → WB → WG → GR), (BR → YO → WO → YG → YR)
22 moves: L R L R L R L (L R' L' R)×2 L' R' L' R' L' R' L'
inverse: L R L R L R L (R' L R L')×2 L' R' L' R' L' R' L'
Move C×2 (square-root inverse of C):
18 moves: L R L R L R L (R' L R L') L' R' L' R' L' R' L'
inverse: L R L R L R L (L R' L' R) L' R' L' R' L' R' L'
Harder method:
By combining algos A, B, and C, you can perform any icosahedral rotation needed to solve the puzzle. There will be an optimal path that can be deduced by tracking the puzzle cycles, orienting the icosahedron visual aid in space to match the puzzle, then undoing the rotations using the algorithms.
Easier method: Tracking icosahedral rotations can be tricky, so instead the symmetries can be reduced further by fixing another point.
- Determine which slot the
YRpiece is in, and perform the appropriate algo to solve it: WGslot: PerformAYGslot: PerformA'BOslot: PerformA ×2WBslot: PerformA' ×2BRslot: PerformBGRslot: PerformB ×2YBslot: PerformB' ×2WOslot: PerformC ×2YOslot: PerformC' ×2
5. Solve triangular symmetry
The remaining pieces express the dihedral group D₆, the symmetry group of an equilateral triangle. Its states include the 3 non-mirrored rotations (0°, 120°, 240°) and the 3 mirrored rotations.
In any mirrored case, only 2-cycles will be present. In this case, use this algorithm to mirror the triangle:
Flip triangle (WB ↔ GR), (BR ↔ YG), (WO ↔ YO), (BO ↔ YB)
12 moves: L R' L' R' L R L' R L R L' R'
Now, the puzzle will either be solved or contain 3-cycles. Execute the triangular rotation algorithm or its inverse to solve the puzzle.
Triangular rotation (WO → BO → GR), (WG → BR → YG), (WB → YB → YO)
16 moves: L' R' (L' R)×2 (L R)×2 L' R' (L R')×2
inverse: (R L')×2 R L (R' L')×2 (R' L)×2 R L
The Crammed Cube is now solved. If this last step didn’t seem to work, revisit step 3 to make sure the WR pieces aren’t switched.
Listing Cycles Procedure
- Looking at any unsolved edge piece, write down its color combination (#1), followed by the color combination of the slot that it’s in (#2)
- Then find the edge piece whose colors match the last entry (#2), and note which slot it’s in…
- Repeat step 2 until you get back to the piece you started with. The number of unique pieces in the list is the order of the cycle (e.g. a 2-cycle or a 6-cycle)
- List out any other cycles until all the edges are accounted for
Gallery
