Updated 2025-07-31
The Quaternion Cube is a rather easy-to-solve puzzle that I designed to visually demonstrate the Quaternion Group Q₈.
Simulator
The puzzle turns over the top 4 vertices of a cube, with 1:2 gearing connecting the opposing corners. There are linear slides under the edge pieces that prevent the static corners from blocking the overall movement.
The puzzle has 24 possible positions, which express the group SL(2,3), isomophic to the group formed by multiplication of the unit Hurwitz quaternions. SL(2,3) contains the Quaternion Group (Q₈) as a subgroup, and these Q₈ states are expressed over the 8 edges whenever the corners are solved.
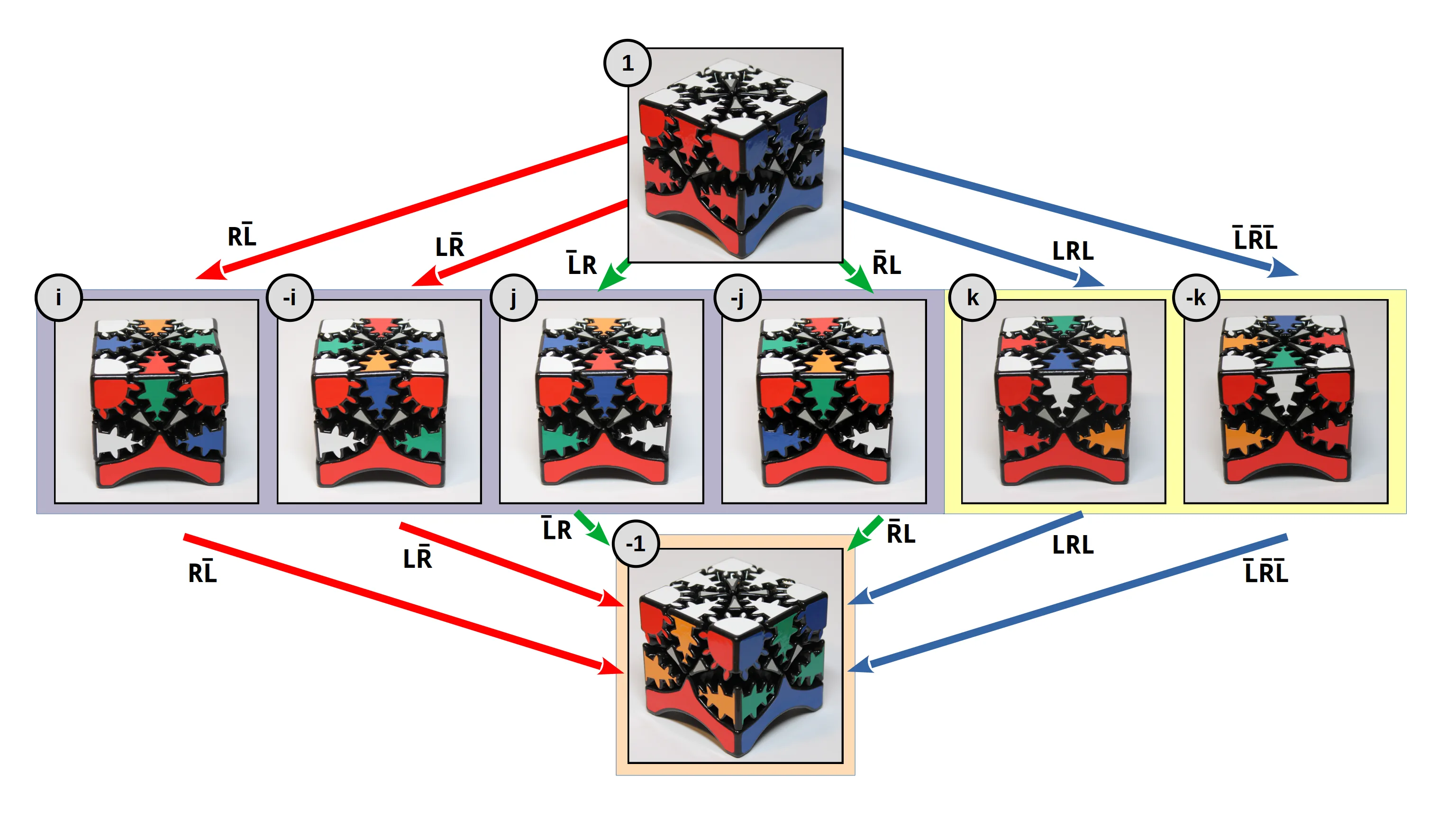
Every 3 turns in the same direction is a corner-preserving sequence, and these sequences can be assigned to the elements i, j, and k of quaternion algebra to construct a graph. Notable is a common ‘inverted state’ that is reachable by repeating any of the 6 intermediate sequences.
By playing with the puzzle you can observe the parallels between quaternion algebra rules and the positions of the edge pieces.
Gallery
Quaternions
Quaternions are a 4-dimensional extension of complex numbers, discovered by Irish mathematician Sir William Rowan Hamilton in 1843. They can be expressed as:
q = a + bi + cj + dk
where a, b, c, d are real numbers and i, j, k are the fundamental quaternion units satisfying i^2 = j^2 = k^2 = ijk = -1.
While initially developed as a mathematical curiosity, quaternion multiplication has become essential in modern 3D computer graphics and robotics for representing rotations.
Hurwitz Quaternions
A comment on the YouTube video pointed out that the SL(2,3) group expressed by the Quaternion Cube is isomorphic to the group formed by multiplication of the unit Hurwitz quaternions.
‘Order’
There are five different orders of unit Hurwitz quaternions: 1, 2, 3, 4, and 6; On the puzzle, the order represents how many times a sequence must be repeated to return to where you started.
Square roots
An unusual property of the unit Hurwitz quaternions is that every order 3 element has a unique square root of order 6. For the single left turn:
L→½(-1+i+j+k)(order 3)
Its square root is:
R̅LR̅→½(+1+i+j+k)(order 6).
Repeating R̅LR̅ twice has the same effect as L.
Selected sequences
| Sequence | Quaternion | Order |
|---|---|---|
| Identity | 1 | 1 |
| L | ½(-1+i+j+k) | 3 |
| R | ½(-1-i-j+k) | 3 |
| R̅LR̅ = sqrt(L) | ½(+1+i+j+k) | 6 |
| L̅RL̅ = sqrt(R) | ½(+1-i-j+k) | 6 |
| RL̅ | i | 4 |
| L̅R | j | 4 |
| RLR or LRL | k | 4 |
| RL̅RL̅ or L̅RL̅R | -1 | 2 |
