The Crammed Cube is an internally geared twisty puzzle that expresses the Mathieu M11 group over its 12 edge pieces. The puzzle features a modified Compy Cube mechanism with 6 axes, which are mechanically linked into two sets using universal joints and gears. It is called the ‘Crammed Cube’ because, while the axis system would normally have 11 moving edges, I’ve crammed an extra one into the red/white edge and lifted the corner angle to make space. This edge duplication is necessary to make the group actions fit over cubic geometry.
Originally published 2025-03-06
Updated 2025-11-05
Video
Solving Guide
Photos

The M12 Cube is an internally geared twisty puzzle that expresses the Mathieu M12 group over its 12 edge pieces.
Video
Solving Guide
Photos

Video: https://www.youtube.com/watch?v=rPHlY3ExgLc
The Triskelion Barrel is another entry in my group theory showcase, this time expressing the PSL₃(3) group over the 13 equilateral triangle pieces. The circles are divided into synchronized sets (marked with red, green, and blue diamond stickers) that turn simultaneously in 180° increments.
I geared the circles together with an external ring gear. Spinning a colored ring causes the corresponding circles to rotate. The mechanism is assembled using a 3D printed kit of axles, bevel gears, and metal pins assembled in layers.
Introduction
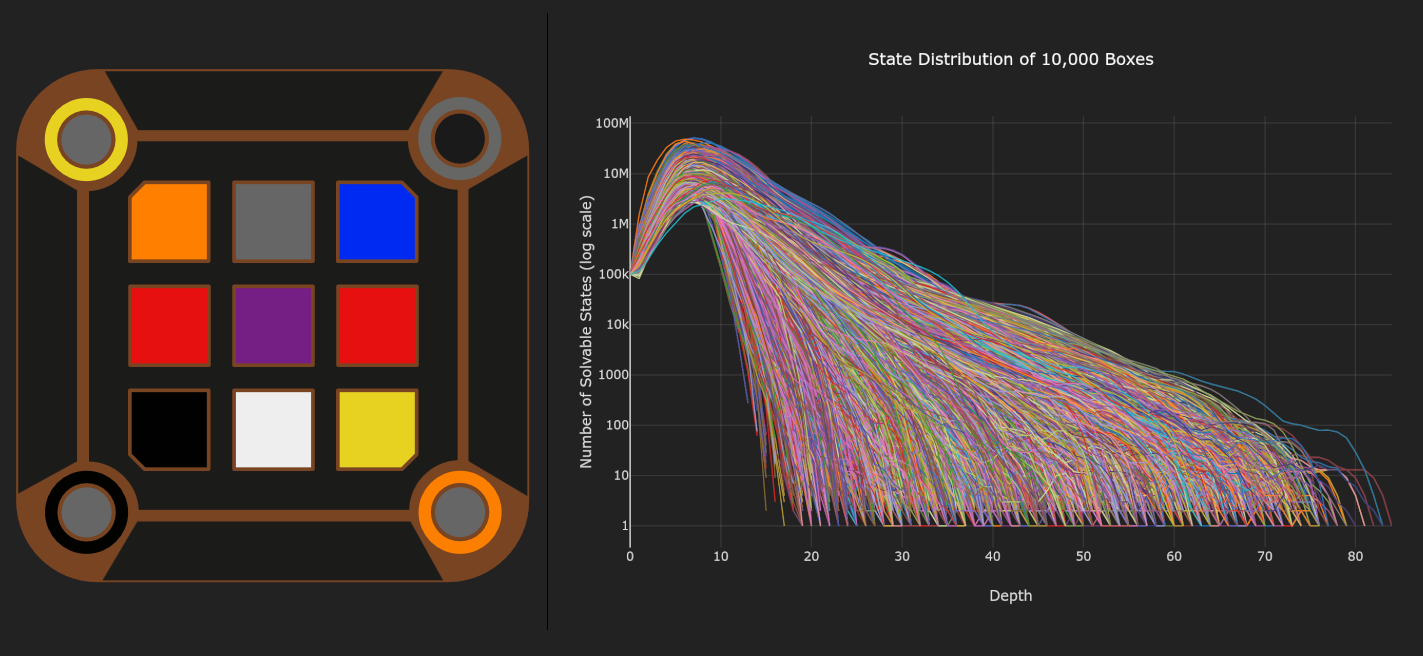
Mora Jai boxes are simple-looking puzzles that can be configured into a huge variety of challenges. The original set of puzzles from Blue Prince mostly have short, simple solutions (2-20 moves), but lengthy and difficult solutions can be constructed by exploring deeper state spaces of the tile grid.
Initially, I wanted to create a list of the most difficult configurations by cataloging the longest solutions, but it turns out that length is not the best predictor of difficulty. Many of the longest solutions rely on repetitive patterns rather than complex logic and novel mechanics.
Ultimately, the list of Challenge puzzles in my simulator was found using a combination of brute-force search, automated filtering, and manual inspection.

Mora Jai Box
A Mora Jai Box is a lock box that involves solving a 3x3 grid of colored tiles. Each color has a unique behavior (see rules). They are originally found in the puzzle/adventure game Blue Prince, but are interesting to analyze on their own.

Introduction
This page documents ongoing attempts to produce a rich, variegated green glaze using an iron/phosphorus mechanism in cone 6 borosilicate glaze.
Some key takeaways so far:
- A lithium-rich base produces a better green than a soda or potash base
- A small addition of lanthanum oxide appears to brighten the effect without changing the color
Iron/Phosphorus Glaze
Blue Hare, Hare’s Fur, or Floating Blue is a widely used effect in pottery studio glazes and commercial glazes.

Video: https://www.youtube.com/watch?v=c0AkCcUzcj8
Print it yourself: https://chandler.io/posts/2025/03/print-it-yourself-illegal-slice-cube/
The Illegal Slice Cube continues my exploration of finite group theory in twisty puzzles. It combines two unusual concepts:
Oskar van Deventer’s Illegal Cube
- Fudging permits 90° turns, which normally wouldn’t be allowed on a 3x3 pentagonal prism.
Slice-only puzzles (like Slice Rex Cube)
- Opposite sides turn simultaneously - like a 3x3 Rubik’s cube with middle turns only.
Unlike some of the previous puzzles in this series, this one is pretty difficult to solve.

STL Files: https://quirkycubes.com/public/Illegal Slice Cube STL.zip
Sticker Template: https://quirkycubes.com/public/Illegal Slice Cube Stickers.zip
Hardware required:
- 4x M3 Springs (~10mm uncompressed)
- 4x M3 Washers
- 4x M3 x 8 Screws (socket or button head)
- 4x M3 x 16 Screws (socket or button head)
- 4x M2 x 8 Button Head Screws
- Lubricant
- Super glue (optional)
The Illegal Slice Cube is easy to print and doesn’t require any special hardware.
Bambu P1S print settings:
- 0.16 mm layers
- Support raft
- Half speed
- Auto snug supports at 25-30°
- Manual strong tree supports on core - just the overhangs
- 3 wall loops (for vapor smoothing)
- Polymaker ABS (Bambu brand ABS does not vapor-smooth)
- Bambu Support for ABS
Assembly
The core is made up of multiple parts that must be assembled in a specific order.
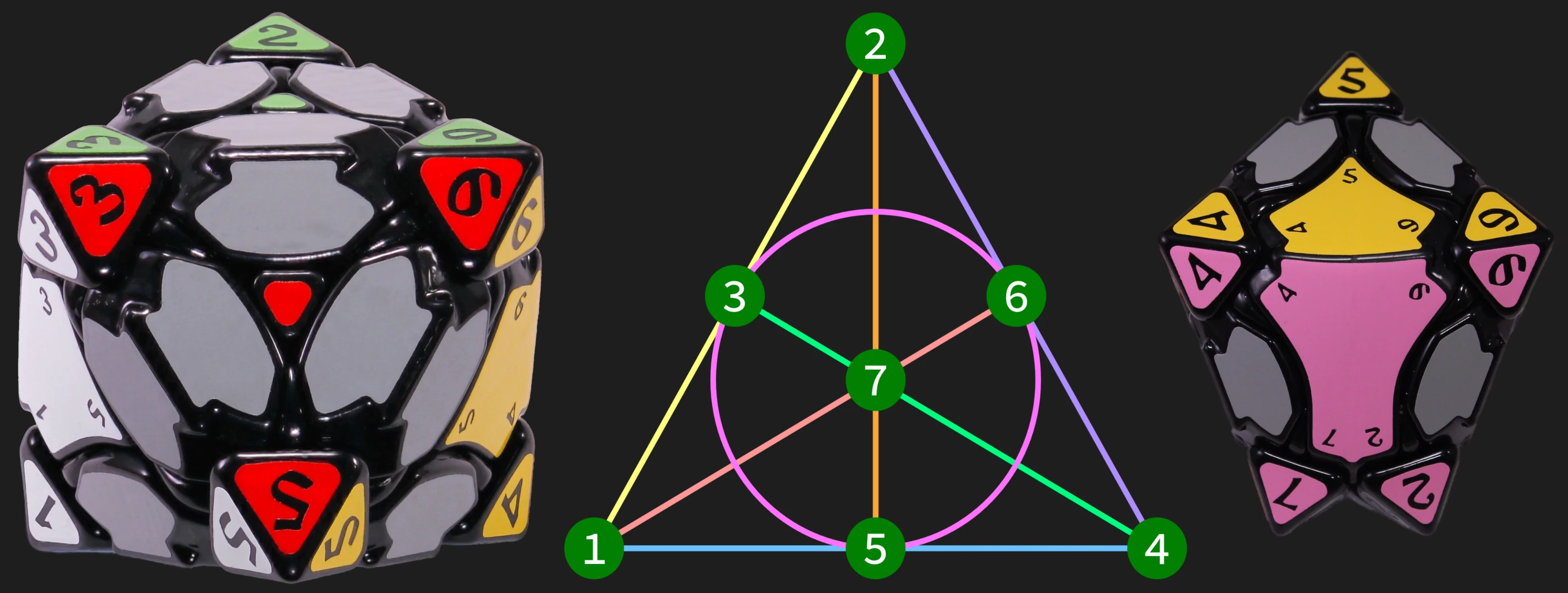
The Fano Gem is a twisty puzzle that I designed to showcase the symmetries of the Fano Plane, which is a familiar object in combinatorics, coding theory, and algebra. The Fano Plane is the smallest possible finite projective plane, constructed from 7 points and 7 lines, where each line contains exactly 3 points.